-
摘要:
目的 拟合新疆维吾尔自治区乌鲁木齐市2020年7月COVID-19疫情流行状况，为疫情防控提供数量依据和理论支撑。 方法 利用仓室建模方法，考虑乌鲁木齐市在2020年7月COVID-19疫情期间所采取的追踪隔离措施，建立具有阶段性控制策略的动力学模型。利用新疆维吾尔自治区卫生健康委员会公布的2020年7-9月COVID-19的累计确诊病例数、累计治愈病例数、累计无症状病例数，使用非线性最小二乘法拟合所建立的模型。 结果 模型的参数估计：确诊速率为0.6，潜伏暴露者类和无症状感染者类的传染力系数分别为0.78和0.99，无症状感染者所占比例为0.4。参数敏感性分析表明，加大密切追踪隔离力度和减少接触能有效控制新增确诊病例。 结论 所建立的模型拟合实际数据效果较好；无症状感染者传染性较强；每日有效再生数变化趋势表明政府控制措施得当，控制效果较好；相关部门应加大密切追踪隔离力度、持续强调减少接触可以有效控制COVID-19的流行。 Abstract:Objective To fit the epidemic situation of COVID-19 in Urumqi City, Xinjiang Uygur Autonomous Region in July 2020, so as to provide the quantitative and theoretical basis for the prevention and control of epidemic. Methods A dynamical model with stage control strategy was proposed using compartmental modeling method, based on the tracking and isolation measures taken during the COVID-19 epidemic in July 2020 in Urumqi City. The nonlinear least square method was applied to fit this dynamical model by using multi-source data: the cumulative number of confirmed cases, cured cases and asymptomatic cases of COVID-19 from Health Committee of Xinjiang from July to September 2020. Results The parameters of the model were estimated as follows: the rate of diagnosis was 0.6, the infectivity coefficients of latent exposure group and asymptomatic infection group were 0.78 and 0.99 respectively, and the proportion of asymptomatic infection group was 0.4. Parameter sensitivity analysis showed that increasing close tracking and isolation and reducing contact could effectively control the number of new confirmed cases. Conclusion The results show that the model has good fitting effect with the actual data; asymptomatic infection is more infectious; the trend of daily effective reproduction number shows that the government control measures are appropriate with great effect; the relevant departments should increase the close tracking and isolation, and continuously emphasize that reducing contact can effectively control the epidemic of COVID-19. -
COVID-19是由新型冠状病毒(2019-nCoV)引发的急性呼吸道传染性疾病[1]。自2019年以来，已经在全球200多个国家和地区发现COVID-19疫情，且其感染病例的数量还在逐步上升[2]。中国COVID-19疫情已经得到基本控制，仅个别地区出现局部暴发和少数境外输入病例[1]。
针对COVID-19疫情大流行，很多学者从各个方面比如数学建模[3-5]、病毒学[6]、流行病学[7]等方法进行了研究和报道。Tang等[3]研究结果表明加强密切接触者追踪、检疫隔离可有效降低传播风险。Tang等[4]在已有研究[3]的基础上建立一类考虑时变接触率和确诊率的动力学模型，其结果表明流行趋势主要取决于隔离和疑似病例。Feng等[5]建立一类包含阶段调整措施的动力学模型，估计韩国疫情将在4月下旬结束，发现改变接触率和检测速度会对峰值大小和峰值达到时间产生影响。
考虑到此次疫情出现大量的无症状感染者和确诊病例并且及时地实施了“封城”措施和多次大规模核酸检测，本文基于多源数据建立具有阶段性控制策略的动力学模型来描述COVID-19在乌鲁木齐市的传播动态，估计疫情的基本再生数并评估相应措施的有效性，为相关部门应对后续波动的疫情提供参考和决策的数量依据和理论支撑。
1. 资料与方法
1.1 资料来源
本文获取了新疆维吾尔自治区卫生健康委员会乌鲁木齐市第二次COVID-19疫情通报信息数据[8]，数据包括从2020年7月15日至2020年9月7日COVID-19的每日新增确诊病例数、每日新增无症状病例数、每日新增治愈病例数、累计确诊病例数、累计无症状病例数、累计治愈病例数、无症状感染者解除医学观察数以及无症状转确诊病例数等。
1.2 模型建立
考虑到乌鲁木齐市第二次疫情期间政府采取的控制措施：包括从7月18日始采取“封城”(乌鲁木齐市)措施，全新疆维吾尔自治区范围内的旅行出行限制和密切接触追踪隔离，以及此次疫情中有大量的无症状感染者且具有传染性，潜伏期人群亦具有传染性[1]等特点。根据传染病动力学仓室建模方法[9]，首先将总人口划分为8个仓室：易感者类(S)、隔离的易感者类(Sq)、潜伏者类(E)、疑似人群类(B=Eq+Sf)、无症状感染者类(A)、有症状感染者类(I)、治愈移出者类(R)及确诊住院者类(H)。根据传播机制，对于S，在接触感染源如E、I或A后，通过密切接触追踪，若以q的概率被追踪到但以(1-β)的概率未被感染则进入到Sq，若以q的概率被追踪到且以β的概率被感染则进入到B，若以(1-q)的概率未被追踪到但以β的概率被感染的S则进入到E中，S也可通过发热门诊以m的发热隔离率进入到B；对于E，若在1/σ的潜伏期后以η的比例转化有症状则进入到I，若在(1/σ)的潜伏期后以(1-η)的比例转化且无症状则进入到A；对于Sq，在1/λ的隔离期满后若未见异常则解除隔离，重新进入到S；对于B，若以b的检测率和f的检出率被检出阳性则进入H，以(1-f)的未被检出率未检出的则重新进入到S；A和I以δA和δI的确诊速率被确诊的进入H进行治疗，存在部分A和I以γA和γI的康复速率进入到R；H以γH的康复速率进入到R，这里认为H已经被隔离治疗，不具备传播条件；总人口N=S+Sq+E+B+A+I+H+R。由于此次疫情持续时间短，且“封城”措施及时，故不考虑自然出生和自然死亡(自然输入和自然输出)以及旅行输出和输入的影响。COVID-19的传播流程图见图 1，模型其他参数和意义见表 1。
图 1 2020年7-9月乌鲁木齐市考虑隔离措施和无症状感染者类的COVID-19传播流程Figure 1. Flow chart of COVID-19 transmission considering isolation measures and asymptomatic cases in Urumqi City from July to September 2020表 1 模型参数估计及其含义Table 1. Model parameter estimation and its meaning参数 含义 值 来源 S(0) 初始S人数 37 000 参数估计 E(0) 初始E人数 26(25.11) 参数估计 I(0) 初始I人数 12(11.328) 参数估计 A(0) 初始A人数 4(3.4) 参数估计 R(0) 初始R人数 0 已有研究[8] H(0) 初始H人数 0 已有研究[8] Sq(0) 初始Sq(无被传染风险) 0 已有研究[8] B(0) 初始B人数 0 已有研究[8] q 接触者隔离率 0.33 参数估计 β 每次接触传播概率 0.07 参数估计 c0 疾病暴发早期接触数 18.00 参数估计 cb 防控策略实施后的最小接触数 2.00 参数估计 r1 接触数的指数下降率 0.24 参数估计 m 通过发热门诊进入B的隔离率 0.07 参数估计 b B检测率 5.5×10-15 参数估计 f 疑似病例的检出率 0.91 参数估计 ε E传染力系数 0.78 参数估计 θ A传染力系数 0.99 参数估计 λ 解除隔离率 1/14 已有研究[3] γA A移出速率 0.10 已有研究[12] γI I移出速率 0.10 已有研究[12] γH H移出速率 0.10 已有研究[12] δA 从A到H的确诊速率 0.60 参数估计 δI 从I到H的确诊速率 0.60 参数估计 d 因病死亡率 0.019 参数估计 η I占感染者的比例 0.60 参数估计 σ E进展为感染者的速率(潜伏期的倒数) 1/7 已有研究[3] 依据疫情传播流程图构建模型，其微分方程组见公式(1)：
$$ \left\{\begin{array} { l } { \frac { \mathrm { d } S } { \mathrm { d } t } = \lambda S q + b ( 1 - f ) B - \frac { q ( 1 - \beta ) c ( t ) S ( I + \varepsilon E + \theta A ) } { N } - } \\ { \frac { ( 1 - q ) \beta c ( t ) \mathrm { S } ( I + \varepsilon E + \theta A ) } { N } - \frac { q \beta c ( t ) S ( I + \varepsilon E + \theta A ) } { N } - m S } \\ { \frac { \mathrm { d } S q } { \mathrm { d } t } = \frac { q ( 1 - \beta ) c ( t ) S ( I + \varepsilon E + \theta A ) } { N } - \lambda S q } \\ { \frac { \mathrm { d } E } { \mathrm { d } t } = \frac { ( 1 - q ) \beta c ( \mathrm { t } ) S ( I + \varepsilon E + \theta A ) } { N } - \sigma E } \\ { \frac { \mathrm { d } B } { \mathrm { d } t } = \frac { q \beta c ( t ) S ( I + \varepsilon E + \theta A ) } { N } - b B + m S } \end{array} \quad \left\{\begin{array}{l} \frac{\mathrm{d} A}{\mathrm{~d} t}=\sigma(1-\eta) E-\delta_{A} A-\gamma_{A} A-d A \\ \frac{\mathrm{d} I}{\mathrm{~d} t}=\sigma \eta E-\delta_{I} I-\gamma_{I} I-d I \\ \frac{\mathrm{d} H}{\mathrm{~d} t}=\delta_{A} A+\delta_{I} I+b f B-\gamma_{H} H-d H \\ \frac{\mathrm{d} R}{\mathrm{~d} t}=\gamma_{A} A+\gamma_{I} I+\gamma_{H} H \\ N=S+S q+E+B+A+I+H+R \end{array}\right.\right. $$ (1) 下面，计算模型的基本再生数和有效再生数：首先当c(t)=c0时，使用下一代再生矩阵方法计算模型基本再生数，采用Wang等[10]的记法，记
$$ F=\left[\begin{array}{c} \frac{(1-q) \beta c(t) S(I+\varepsilon E+\theta A)}{N} \\ \frac{q \beta c(t) S(I+\varepsilon E+\theta A)}{N} \\ 0 \\ 0 \end{array}\right], \quad V=\left[\begin{array}{c} \sigma E \\ b B-m S \\ \delta_{A} A+y_{A} A+d A-\sigma(1-\eta) E \\ \delta_{I} I+\gamma_{I} I+d I-\sigma \eta E \end{array}\right] , $$ 其中
$$ c(t)=\left\{\begin{array}{l} c_{0}, t<4 \\ \left(c_{0}-c_{b}\right) \times e^{-r_{1}(t-3)}+c_{b}, \quad \geq 4 \end{array}\right. ; $$ 进一步，对F和V在无病平衡点处求关于E、B、A和I的偏导，得
$$ \begin{array}{c} F(t)=\left[\begin{array}{cccc} \frac{(1-q) \beta c(t) S \varepsilon N-(1-q) \beta c(t) S \omega}{N^{2}} & \frac{-(1-q) \beta c(t) S \omega}{N^{2}} & \frac{(1-q) \beta c(t) S \theta N-(1-q) \beta c(t) S \omega}{N^{2}} & \frac{(1-q) \beta c(t) S N-(1-q) \beta c(t) S \omega}{N^{2}} \\ \frac{q \beta c(t) S \varepsilon N-q \beta c(t) S \omega}{N^{2}} & \frac{-q \beta c(t) S \omega}{N^{2}} & \frac{q \beta c(t) S \theta N-q \beta c(t) S \omega}{N^{2}} & \frac{q \beta c(t) S N-q \beta c(t) S \omega}{N^{2}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \\ V(t)=\left[\begin{array}{cccc} \sigma & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ -\sigma(1-\eta) & 0 & \delta_{A}+\gamma_{A}+d & 0 \\ -\sigma \eta & 0 & 0 & \delta_{I}+\gamma_{I}+d \end{array}\right] \end{array}. $$ 其中ω=I+εE+θA；则下一代再生矩阵定义为
$$ F V^{-1}=\left[\begin{array}{cccc} \frac{(1-q) \beta c(t) \varepsilon}{\sigma}+\frac{(1-q) \beta c(t) \theta(1-\eta)}{\delta_{A}+\gamma_{A}+d}+\frac{(1-q) \beta c(t) \eta}{\delta_{I}+\gamma_{I}+d} & 0 & \frac{(1-q) \beta c(t) \theta}{\delta_{A}+\gamma_{A}+d} & \frac{(1-q) \beta c(t)}{\delta_{I}+\gamma_{I}+d} \\ \frac{q \beta c(t) \varepsilon}{\sigma}+\frac{(1-\eta) q \beta c(t) \theta}{\delta_{A}+\gamma_{A}+d}+\frac{q \beta c(t)}{\delta_{I}+\gamma_{I}+d} & 0 & \frac{q \beta c(t) \theta}{\delta_{A}+\gamma_{A}+d} & \frac{q \beta c(t)}{\delta_{I}+\gamma_{I}+d} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], $$ 因此，模型(1)的基本再生数R0定义如下：
$$ \begin{aligned} R_{0}=& \rho\left(F V^{-1}\right)=(1-q) * \beta * c_{0} * \varepsilon / \sigma+(1-q) * \beta * \\ & c_{0} * \theta *(1-\eta) /\left(\delta_{A}+\gamma_{A}+d\right)+(1-q) * \beta * c_{0} * \eta / \\ &\left(\delta_{I}+\gamma_{I}+d\right) \end{aligned} $$ 其中ρ(FV-1) 为矩阵FV-1的谱半径。
其次，当采取相应控制措施时，按Tang等[4]的方法，用随时间变化的接触率c(t)代替常数接触率c0，因此定义模型(1)的有效再生数Rd(t)定义如下：
$$ \begin{aligned} R_{d}(t)=&(1-q) * \beta * c(t) * \varepsilon / \sigma+(1-q) * \beta * c(t) * \theta \\ & *(1-\eta) /\left(\delta_{A}+\gamma_{A}+d\right)+(1-q) * \beta * c(t) * \eta /\left(\delta_{I}\right.\\ &\left.+\gamma_{I}+d\right) . \end{aligned} $$ 有效再生数Rd(t)可以用来衡量传染病控制的情况，当Rd(t)>1时，说明控制措施及其强度还不足，疾病将继续流行；Rd(t) < 1，说明疾病已被控制，在一定时间内将消亡。
1.3 误差估计
采用平均绝对百分比误差(mean absolute percentage error, MAPE)和均方根百分比误差(root mean square percent error, RMSPE)来评价所建立模型的拟合效果或精准度：误差≥50%为拟合度差，50%>误差≥20%为拟合合理，20%>误差≥10%为拟合较好，误差 < 10%为拟合精准。MAPE和RMSPE的定义分别为：
$$ \begin{array}{l} \operatorname{MAPE}=\left(\frac{1}{n} \sum\limits_{t=2}^{n} \mid \frac{W(t)^{*}-W(t)}{W(t)^{*}}\right) \times 100 \%, \\ \mathrm{RMSPE}=\sqrt{\frac{\sum\limits_{t=2}^{n}\left(\frac{W(t)^{*}-W(t)}{\left.W(t)^{*}\right)^{2}}\right.}{n-1}} \times 100 \%, \end{array} $$ 其中，W(t)*和W(t)分别为t时刻的实际值和拟合值，n为用于拟合的数据个数。
2. 结果
2.1 模型参数估计
本文记Y1(t)表示在时间t时的累计无症状病例数，记Y2(t)表示时间t时的累计确诊病例数，记Y3(t)表示时间t时累计治愈病例数；则dY1(t)/dt=δA A+γA A+dA，dY2(t)/dt=γH H+dH，dY3(t)/dt=γA A+γI I+γH H。
本文将2020年7月15日出现第一例确诊病例至7月17日没有实施“封城”措施的3 d当作乌鲁木齐市第二次COVID-19疫情的第一阶段，将7月18日始至9月7日第二次疫情结束(即所有病例治愈出院或解除医学观察)作为第二阶段。在第二阶段，为了切断传播渠道，乌鲁木齐市疫情防控工作聚焦重点人群和重点部位，采取了严格的管控措施。根据新疆维吾尔自治区2020年统计年鉴[11]，乌鲁木齐市常住人口约为335.2万人，但由于1个COVID-19感染者在其感染期内的活动范围和接触人员有限，因此将常住人口当做S不符实际，基于此，本文估计初始S约为37 000人。估计出初始的E、I和A分别约为26、12和4人。初始B、初始Sq、初始H、初始R根据新疆维吾尔自治区卫生健康委员会关于COVID-19疫情的通报信息确定为0人。另隔离人群在为期14 d的隔离医学观察未见异常者则解除隔离，因此λ=1/14；COVID-19的潜伏期约为7 d，因此取σ =1/7。把初始接触率假定为2020年7月15日到7月17日之间的平均接触率c0，假设第二阶段除了接触率(数)发生改变外，其他参数与第一阶段保持相同。模型其他的参数估计或取值见表 1。
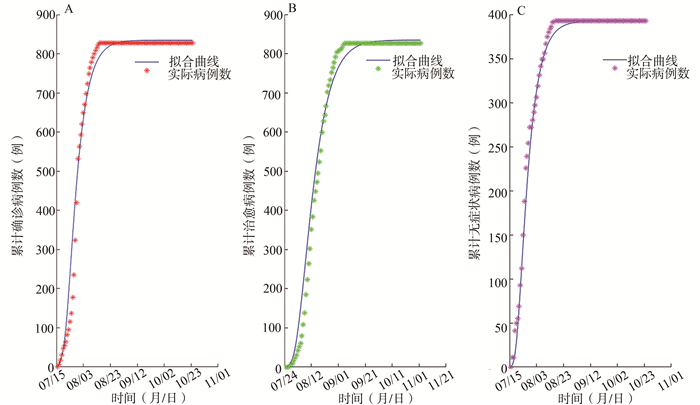
采用非线性最小二乘法[5]同时拟合这三组实际累计数据，使用MATLABR 2017b软件进行模型拟合和参数估计，使用R 4.0.5软件实现部分结果的可视化。见图 2。
图 2 2020年7-9月COVID-19乌鲁木齐市累计确诊(A)、累计治愈(B)、累计无症状病例数(C)与模型(1)的拟合图Figure 2. Fitting diagram of cumulative number of confirmed cases(A)、cumulative number of cured cases(B) and cumulative number of asymptomatic cases(C) of COVID-19 in Urumqi City in July to September 2020 with model (1)2.2 模型评价
计算得到三组数据的MAPE和RMSPE值(见表 2)，由此可知模型(1)拟合的效果较好，可利用该模型对乌鲁木齐市COVID-19疫情流行状况进行拟合。为了估计每日有效再生数，本文首先得到随时间变化的接触率c(t)，进而使用接触率c(t)的离散值计算出每日的有效再生数。2020年7月15日到7月17日之间COVID-19的平均(初始)接触率为18，对应该时间段的Rd(t)点估计值为R0=6.24；在2020年7月30日，c(t)降到2.71，此时Rd(t)降到1以下，即新感染的数量已开始下降；此后c(t)、Rd(t)分别趋近并稳定在2.00和0.69。值得注意的是，数值模拟实验发现实际累计治愈数与模型中累计治愈拟合曲线有为期10 d的迟滞时间。当模型参数固定后，将模型在累计治愈数上向后平移10 d，模型与数据拟合较好。模型估计在7月18日即有治愈病例，实际至7月28日才有第1例治愈病例。第1例确诊病例(7月15日出现)在为期14 d的医学治疗和观察无异常后转为治愈病例，这个时间与COVID-19诊疗方案(试行第八版)[1]中说明的潜伏期为1~14 d的最多潜伏天数相吻合。见表 2。
表 2 MAPE和RMSPE评价结果Table 2. Evaluation results of MAPE and RMSPE比较对象 MAPE(RMSPE) (%) 拟合结果 实际确诊与拟合确诊 8.36(23.39) 精准(合理) 实际治愈与拟合治愈 17.13(41.70) 较好(合理) 实际无症状与拟合无症状 3.16(9.57) 精准(精准) 2.3 参数的敏感性分析
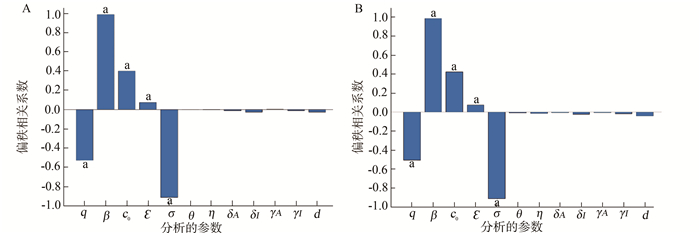
考虑模型(1)的参数q、β、c0、ε、σ、θ、η、δA、δI、γA、γI和d对基本再生数R0的影响，如图 3所示。可知q和σ对R0有负影响，β、c0和ε对R0有正影响，其他参数对R0无影响，其中参数β的偏相关系数绝对值最大，ε的偏相关系数绝对值最小。通过敏感性分析可以得出，有效控制参数q、σ、c0、β和ε能对COVID-19的流行产生影响。
图 3 参数的偏相关系数值[(A)10 000次、(B)12 000次)]注：a表示影响有统计学意义的参数。Figure 3. Partial rank correlation coefficient values of parameters [(A)10 000 times、(B)12 000 times)]2.4 疾病的控制
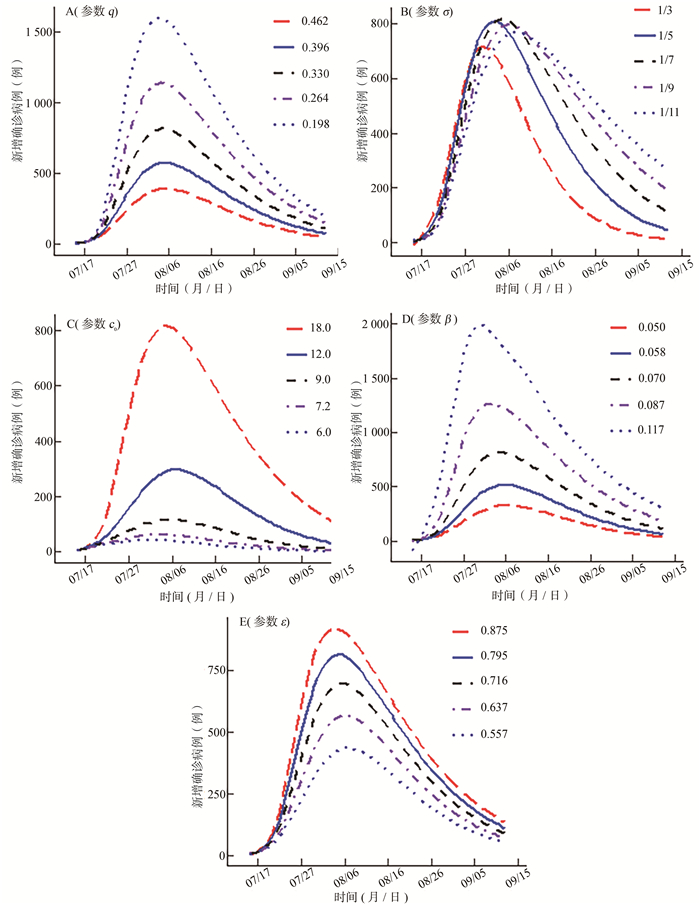
参数q、σ、c0、β和ε对新增确诊病例数可能存在影响。(1)当q分别取值0.198、0.264、0.330、0.396和0.462时，新增确诊病例数随着q的增大越来越小，见图 4A。这表明接触者隔离率q越大，新增确诊病例越少。(2)当σ分别取值1/3、1/5、1/7、1/9和1/11时，新增确诊病例数达到峰值的时间随着σ的减小而延后，见图 4B，但σ的变化对新增确诊病例数峰值的变化影响不大。这表明当COVID-19潜伏期越长，则新增确诊病例数达到峰值的时间越晚，这是符合实际的。(3)当c0分别取值18.00、12.00、9.00、7.20和6.00时，新增确诊病例数随着c0的减小而减小，见图 4C，且当c0从18.00减小到12.00时，新增确诊病例数减小幅度较大。这表明减少疾病暴发早期接触，能有效减少新增确诊病例数。(4)当β分别取值0.117、0.087、0.070、0.058和0.050时，新增确诊病例数随着β的增大而越来越小，见图 4D。这表明每次接触传播概率β越大，新增确诊病例越多。(5)当ε分别取值0.875、0.795、0.716、0.637和0.557时，新增确诊病例数随着ε增大而越来越多，见图 4E。这表明若潜伏期人群传染力系数越大，则感染人数越多。综上，参数q、σ、c0、β和ε的敏感性分析表明，加大对密切接触者的追踪隔离力度和强调减少接触可有效降低感染人数。
图 4 参数q、σ、c0、β和ε对COVID-19新增确诊病例数的影响Figure 4. The influence of parameters q, σ, c0, β and ε on the number of new confirmed cases of COVID-193. 讨论
乌鲁木齐市从2020年4月全面恢复生产秩序以来，进出境旅客数量大、管控难度高，于2020年7月15日暴发了第二次COVID-19疫情，自7月15日确认第1例确诊病例至9月7日所有确诊病例全部治愈并解除医学观察，共持续55 d。受到相关研究[3-5]启发，考虑到在乌鲁木齐市此次疫情中存在大量的无症状感染者，本文考虑了A仓室，并对A的传染性作了定量估计。
在早期的研究中，由于对COVID-19传播机制、临床特征了解不充分等原因，Feng等[5]、唐等[13]针对疫情传播分别建立了确定性动力学模型和离散动力学模型，但在模型中都未考虑A对疫情传播的影响。本文估计出此次疫情中7月15日Rd(t)的点估计值为6.24，高于Feng等[5]、唐等[13]的研究结果。Tang等[3-4]在模型中引入了A仓室，得到Rd(t)为6.39和6.47。因此在建模过程中考虑A对疫情传播的影响，是符合COVID-19传播机制和实际情况的。
本文基于乌鲁木齐市7月至9月COVID-19疫情的累计确诊病例数、累计无症状病例数、累计治愈病例数三组多源数据，利用仓室建模方法，考虑在疫情期间政府所采取的追踪隔离等措施，建立具有阶段性控制策略的动力学模型。利用该多源数据拟合所建立的动力学模型，拟合效果较好。并且估计从感染者能被检测到确诊的速率为0.6，即约为1.67 d的时间即可确诊，这体现了乌鲁木齐市多次实施大规模全员核酸检测工作的成效，更快的检测出感染者进而确诊对于疫情控制具有重要意义；估计E和A的传染力系数分别为0.78和0.99，A的传染性和I的传染性基本一致，且A所占比例大。
相比于Tang等[3-4]、唐等[13]的研究，本文根据感染者临床特征对E的传染性也作了估计，估计E的传染力系数为0.78，与Feng等[5]的研究结果E的传染性为0.53相近。E和A的传染性分析结果提示在疫情防控过程中不能只关注I，E和A具有传染性又无症状且在人群中不易被识别，说明在疫情尚未完全结束之前应当保持或加大核酸检测频率以便更快地检出E和A并对其进行隔离观察。此外，参数q、σ、c0、β和ε的敏感性分析表明加大密切接触者追踪隔离力度和减少接触是控制COVID-19传播的有效途径。
本文也具有局限性：本文只考虑了在控制措施变化下接触率的变化，并未考虑在医疗资源倾斜和改善状况下的确诊率的变化，在治疗、护理条件改善情况下恢复率的变化，以及疫情期间群众防范意识提高对于接触率和自我隔离的影响，这些问题值得进一步展开研究。
-
图 1 2020年7-9月乌鲁木齐市考虑隔离措施和无症状感染者类的COVID-19传播流程
Figure 1. Flow chart of COVID-19 transmission considering isolation measures and asymptomatic cases in Urumqi City from July to September 2020
图 2 2020年7-9月COVID-19乌鲁木齐市累计确诊(A)、累计治愈(B)、累计无症状病例数(C)与模型(1)的拟合图
Figure 2. Fitting diagram of cumulative number of confirmed cases(A)、cumulative number of cured cases(B) and cumulative number of asymptomatic cases(C) of COVID-19 in Urumqi City in July to September 2020 with model (1)
图 3 参数的偏相关系数值[(A)10 000次、(B)12 000次)]
注：a表示影响有统计学意义的参数。
Figure 3. Partial rank correlation coefficient values of parameters [(A)10 000 times、(B)12 000 times)]
图 4 参数q、σ、c0、β和ε对COVID-19新增确诊病例数的影响
Figure 4. The influence of parameters q, σ, c0, β and ε on the number of new confirmed cases of COVID-19
表 1 模型参数估计及其含义
Table 1. Model parameter estimation and its meaning
参数 含义 值 来源 S(0) 初始S人数 37 000 参数估计 E(0) 初始E人数 26(25.11) 参数估计 I(0) 初始I人数 12(11.328) 参数估计 A(0) 初始A人数 4(3.4) 参数估计 R(0) 初始R人数 0 已有研究[8] H(0) 初始H人数 0 已有研究[8] Sq(0) 初始Sq(无被传染风险) 0 已有研究[8] B(0) 初始B人数 0 已有研究[8] q 接触者隔离率 0.33 参数估计 β 每次接触传播概率 0.07 参数估计 c0 疾病暴发早期接触数 18.00 参数估计 cb 防控策略实施后的最小接触数 2.00 参数估计 r1 接触数的指数下降率 0.24 参数估计 m 通过发热门诊进入B的隔离率 0.07 参数估计 b B检测率 5.5×10-15 参数估计 f 疑似病例的检出率 0.91 参数估计 ε E传染力系数 0.78 参数估计 θ A传染力系数 0.99 参数估计 λ 解除隔离率 1/14 已有研究[3] γA A移出速率 0.10 已有研究[12] γI I移出速率 0.10 已有研究[12] γH H移出速率 0.10 已有研究[12] δA 从A到H的确诊速率 0.60 参数估计 δI 从I到H的确诊速率 0.60 参数估计 d 因病死亡率 0.019 参数估计 η I占感染者的比例 0.60 参数估计 σ E进展为感染者的速率(潜伏期的倒数) 1/7 已有研究[3] 
下载: 导出CSV
表 2 MAPE和RMSPE评价结果
Table 2. Evaluation results of MAPE and RMSPE
比较对象 MAPE(RMSPE) (%) 拟合结果 实际确诊与拟合确诊 8.36(23.39) 精准(合理) 实际治愈与拟合治愈 17.13(41.70) 较好(合理) 实际无症状与拟合无症状 3.16(9.57) 精准(精准)
下载: 导出CSV
-
[1] 中华人民共和国国家卫生健康委员会. 新型冠状病毒肺炎诊疗方案(试行第八版)[J]. 中华临床感染病杂志, 2020, 13(5): 321-328. DOI: 10.3760/cma.j.issn.1674-2397.2020.05.001.National Health Commission of the People's Republic of China. COVID-19 diagnosis and treatment plan (trial eighth edition)[J]. Chin J Clin Infect Dis, 2020, 13(5): 321-328. DOI: 10.3760/cma.j.issn.1674-2397.2020.05.001. [2] 白宁, 宋晨玮, 徐瑞. 基于动力学模型的COVID-19疫情预测与控制策略研究[J]. 应用数学学报, 2020, 43(3): 483-493. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSU202003001.htmBai N, Song CW, Xu R. Predicting the trend and evaluating control strategies of COVID-19 based on a dynamical model[J]. Acta Math Appl Sin, 2020, 43(3): 483-493 https://www.cnki.com.cn/Article/CJFDTOTAL-YYSU202003001.htm [3] Tang B, Wang X, Li Q, et al. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions[J]. J Clin Med, 2020, 9(2): E462. DOI: 10.3390/jcm9020462. [4] Tang B, Bragazzi NL, Li Q, et al. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCoV)[J]. Infect Dis Model, 2020, 5: 248-255. DOI: 10.1016/j.idm.2020.02.001. [5] Feng XM, Chen J, Wang K, et al. Phase-adjusted estimation of the COVID-19 outbreak in South Korea under multi-source data and adjustment measures: a modelling study[J]. Math Biosci Eng, 2020, 17(4): 3637-3648. DOI: 10.3934/mbe.2020205. [6] 俞骅, 王旭初, 李钧, 等. 杭州市首例新型冠状病毒肺炎病例病毒全基因组序列测定及分析[J]. 中华预防医学杂志, 2020, 54(5): 486-490. DOI: 10.3760/cma.j.cn112150-20200217-00128.Yu H, Wang XC, Li J, et al. Genomic analysis of a 2019-novel coronavirus (2019-nCoV) strain in the first COVID-19 patient found in Hangzhou[J]. Chin J Prev Med, 2020, 54(5): 486-490. DOI: 10.3760/cma.j.cn112150-20200217-00128. [7] 朱正保, 仲崇科, 张凯欣, 等. 中国内地新型冠状病毒肺炎流行趋势分析[J]. 中华预防医学杂志, 2020, 54(6): 620-624. DOI: 10.3760/cma.j.cn112150-20200222-00163.Zhu ZB, Zhong CK, Zhang KX, et al. Epidemic trend of COVID-19 in Chinese mainland[J]. Chin J Prev Med, 2020, 54(6): 620-624. DOI: 10.3760/cma.j.cn112150-20200222-00163. [8] 新疆维吾尔自治区卫生健康委员会. 防控新型冠状病毒肺炎疫情[EB/OL]. (2020-07-15)[2020-09-17]. http://wjw.xinjiang.gov.cn/hfpc/fkxxfy/fkxxfy.shtml.Health Committee of Xinjiang Uygur Autonomous Region. Prevention and control of new coronavirus pneumonia[EB/OL]. (2020-07-15)[2020-09-17]. http://wjw.xinjiang.gov.cn/hfpc/fkxxfy/fkxxfy.shtml. [9] 马知恩, 周义仓, 李建全, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004: 1-20.Ma ZE, Zhou YC, Li JQ, et al. Mathematical modeling and research on dynamics of infectious diseases[M]. Beijing: Science Press, 2004: 1-20. [10] Wang WD, Zhao XQ. Threshold dynamics for compartmental epidemic models in periodic environments[J]. J Dyn Differ Equations, 2008, 20(3): 699-717. DOI: 10.1007/s10884-008-9111-8. [11] 乌鲁木齐市人民政府乌鲁木齐市统计局. 2019年乌鲁木齐市国民经济和社会发展统计公报[EB/OL]. (2020-06-18)[2020-06-18]. http://www.urumqi.gov.cn/fjbm/tjj/tjgb/446900.htm.Urumqi Statistics Bureau of Urumqi Municipal People's Government. Statistical bulletin of national economic and social development of Urumqi in 2019[EB/OL]. (2020-06-18)[2020-06-18]. http://www.urumqi.gov.cn/fjbm/tjj/tjgb/446900.htm. [12] 魏永越, 卢珍珍, 杜志成, 等. 基于改进的SEIR+CAQ传染病动力学模型进行新型冠状病毒肺炎疫情趋势分析[J]. 中华流行病学杂志, 2020, 41(4): 470-474, 475. DOI: 10.3760/cma.j.cn112338-20200216-00106.Wei YY, Lu ZZ, Du ZC, et al. Fitting and forecasting the trend of COVID-19 by SEIR+CAQ dynamic model[J]. Chin J Epidemiol, 2020, 41(4): 470-474, 475. DOI: 10.3760/cma.j.cn112338-20200216-00106. [13] 唐三一, 唐彪, Nicola Luigi Bragazzi, 等. 新型冠状病毒肺炎疫情数据挖掘与离散随机传播动力学模型分析[J]. 中国科学: 数学, 2020, 50(8): 1071-1086. DOI: 10.1360/SSM-2020-0053.Tang SY, Tang B, Bragazzi N, et al. Analysis of COVID-19 epidemic traced data and stochastic discrete transmission dynamic model[J]. Sci Sin Math, 2020, 50(8): 1071-1086. DOI: 10.1360/SSM-2020-0053. 期刊类型引用(2)
1. 王朝阳，刘泉泉，田正福，马佳琪，张利萍. 基于Joinpoint模型的我国和境外输入新型冠状病毒感染趋势对比. 医学信息. 2023(02): 39-42+48 . 
百度学术2. 朱懋昌，宾晟，孙更新. 基于COVID-19传播特性的传染病模型的构建与研究. 复杂系统与复杂性科学. 2023(02): 29-37 . 百度学术其他类型引用(3)
-
下载:
点击查看大图
计量
- 文章访问数: 689
- HTML全文浏览量: 308
- PDF下载量: 97
- 被引次数: 5