倾向性评分逆概率加权中极端权重处理方法的模拟比较及应用研究

许毛毛; 高绒绒; 高倩; 王菊平; 王佳乐; 王彤

doi:10.16462/j.cnki.zhjbkz.2024.01.011

倾向性评分逆概率加权中极端权重处理方法的模拟比较及应用研究

doi: 10.16462/j.cnki.zhjbkz.2024.01.011

山西医科大学公共卫生学院卫生统计学教研室，煤炭环境致病与防治教育部重点实验室，太原 030001

基金项目:

国家自然科学基金 82073674

国家自然科学基金 82204163

山西省基础研究计划资助项目 202203021212382

详细信息

通讯作者:
王彤，E-mail: tongwang@sxmu.edu.cn

中图分类号: R195.1
计量
- 文章访问数: 149
- HTML全文浏览量: 69
- PDF下载量: 17
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-11
- 修回日期: 2023-08-26
- 网络出版日期: 2024-02-05
- 刊出日期: 2024-01-10

A simulation comparison and application study of extreme weighting methods in propensity score inverse probability weighting

Department of Health Statistics, School of Public Health, Shanxi Medical University, MOE Key Laboratory of Coal Environmental Pathogenicity and Prevention, Taiyuan 030001, China

Funds:

National Natural Science Foundation of China 82073674

National Natural Science Foundation of China 82204163

Basic Research Project of Shanxi Province 202203021212382

More Information

Corresponding author: WANG Tong, E-mail: tongwang@sxmu.edu.cn

摘要

摘要: 目的通过模拟研究比较倾向性评分逆概率加权法(inverse probability weighting, IPW)及其5种替代方法在有限重叠和倾向评分模型错误指定下的性能，并应用这些方法探讨血清总25-羟基维生素D[25-hydroxyvitamin D, 25(OH)D]缺乏与成年人睡眠时间的关系。方法通过蒙特卡洛模拟，设置不同样本量、倾向性评分重叠度、模型指定情况的模拟场景，比较6种方法的统计性能。结果模拟结果显示，IPW对重叠度差和模型错误指定比较敏感，其替代方法可表现出更强的稳定性和更高的效率，其中重叠权重(overlap weights, OW)法可提供最好的效应估计。血清总25(OH)D缺乏者睡眠时间比血清总25(OH)D充足者少(P < 0.001)。结论 OW可作为存在极端权重时IPW方法的最优替代，血清总25(OH)D缺乏会减少成年人的睡眠时间。
- 倾向性评分 /
- 逆概率加权 /
- 极端权重 /
- 25-羟基维生素D /
- 睡眠时间
Abstract: Objective This paper proposes a simulation study to compare the performance of propensity score inverse probability weighting (IPW) and its five alternatives under limited overlap and propensity score model misspecification. Additionally, it seeks to employ these methods to explore the relationship between serum total 25-hydroxyvitamin D [25(OH)D] deficiency and sleep duration in adults. Methods The statistical performance of these six methods was compared through Monte Carlo simulations by setting up simulation scenarios with different sample sizes, propensity score overlap, and model-specified cases. Results Simulation results showed that IPW is particularly sensitive to differences in overlap and model misspecification, while alternative methods showed greater stability and higher efficiency. Notably, the overlap weights (OW) method provided the most accurate effect estimates. It was observed that adults with total serum 25(OH)D deficiency have shorter sleep duration compared to those with adequate total serum 25(OH)D (P < 0.001). Conclusions The OW method can be used as an optimal alternative to the IPW method in the presence of extreme weights. The study also concludes that serum total 25(OH)D deficiency reduces sleep duration in adults.
- Propensity score /
- Inverse probability weighting /
- Extreme weights /
- 25-hydroxyvitamin D /
- Sleep duration

HTML全文

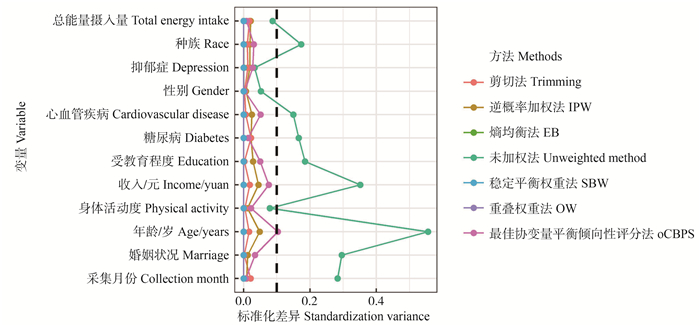
图 1 加权前及加权后2组个体各基线协变量均衡性情况

IPW, 逆概率加权法；EB, 熵均衡法；SBW, 稳定权重值均衡法；OW, 重叠权重法；oCBPS, 最优协变量均衡法。

Figure 1. Balance of baseline covariates of individuals in the two groups before and after weighting

IPW, inverse probability weight; EB, entropy balancing; SBW, stable weights that balance covariates; OW, overlap weights; oCBPS, optimal covariate balancing.

下载: 全尺寸图片幻灯片

表 1 IPW及替代方法在不同重叠度下的模拟表现

Table 1. Simulation performance of IPW and alternative methods under different overlap degrees

重叠度 Degree of overlap	方法 Method	偏倚 Bias	均方根误差 RMSE	s	$ s_{\bar{x}}$	95% CI覆盖率 Coverage probability
好Good	IPW	0.17	9.06	9.06	8.55	0.95
	剪切法Trimming	0.06	7.72	7.73	7.66	0.95
	OW	0.14	6.90	6.90	6.66	0.93
	oCBPS	-0.02	7.34	7.34	6.95	0.93
	EB	0.12	7.00	7.00	19.20	1.00
	SBW	0.16	6.95	6.95	18.26	1.00
中Middle	IPW	1.08	25.09	25.08	17.90	0.89
	剪切法Trimming	0.24	9.44	9.44	9.37	0.95
	OW	0.21	7.52	7.52	7.36	0.94
	oCBPS	0.36	9.49	9.49	15.15	0.98
	EB	0.19	8.17	8.17	22.90	1.00
	SBW	0.33	7.88	7.87	19.48	1.00
差Poor	IPW	7.68	42.25	41.57	27.94	0.76
	剪切法Trimming	0.40	10.13	10.13	10.26	0.96
	OW	0.32	8.05	8.05	8.15	0.95
	oCBPS	1.55	13.01	15.40	76.23	1.00
	EB	0.45	9.36	12.92	26.79	1.00
	SBW	0.55	8.66	9.35	20.84	1.00
注: IPW, 逆概率加权法; OW, 重叠权重法; oCBPS, 最优协变量均衡法; EB, 熵均衡法; SBW, 稳定权重值均衡法; RMSE, 均方根误差。 Note : IPW, inverse probability weight; OW, overlap weights; oCBPS, optimal covariate balancing; EB, entropy balancing; SBW, stable weights that balance covariates; RMSE, root mean square error.

下载: 导出CSV

表 2 IPW及替代方法在模型正确指定和错误指定下的模拟表现

Table 2. Simulation performance of IPW and alternative methods under correct and incorrect model settings

模型设定 Model settings	方法 Method	偏倚 Bias	均方根误差 RMSE	s	$ s_{\bar{x}}$	95% CI覆盖率 Coverage probability
正确Correct	IPW	1.08	25.09	25.08	17.90	0.89
	剪切法Trimming	0.24	9.44	9.44	9.37	0.95
	OW	0.21	7.52	7.52	7.36	0.94
	oCBPS	0.36	9.49	9.49	15.15	0.98
	EB	0.19	8.17	8.17	22.90	1.00
	SBW	0.33	7.88	7.87	19.48	1.00
错误Incorrect	IPW	2.74	25.88	25.75	20.53	0.86
	剪切法Trimming	0.43	9.22	9.22	9.36	0.95
	OW	0.41	7.33	7.33	7.51	0.96
	oCBPS	1.23	9.63	9.55	9.88	0.95
	EB	0.22	7.76	7.76	23.25	1.00
	SBW	0.35	7.55	7.55	18.34	1.00
注: IPW, 逆概率加权法; OW, 重叠权重法; oCBPS, 最优协变量均衡法; EB, 熵均衡法; SBW, 稳定权重值均衡法; RMSE: 均方根误差。 Note : IPW, inverse probability weight; OW, overlap weights; oCBPS, optimal covariate balancing; EB, entropy balancing; SBW, stable weights that balance covariates; RMSE, root mean square error.

下载: 导出CSV

表 3 IPW及替代方法的效应估计

Table 3. Effect estimates of IPW and alternative methods

方法Method	平均处理效应ATE	$s_{\bar{x}} $	95% CI	P值value
未加权	0.117 6	0.049 8	0.019 9~0.215 2	0.018
IPW	0.200 0	0.054 6	0.093 1~0.307 0	< 0.001
剪切法Trimming	0.187 4	0.055 7	0.078 3~0.296 6	< 0.001
OW	0.208 6	0.054 0	0.102 7~0.314 4	< 0.001
oCBPS	0.700 9	0.056 9	0.589 4~0.812 4	0.003
EB	0.206 6	0.055 2	0.098 4~0.314 8	< 0.001
SBW	0.225 2	0.055 7	0.116 0~0.334 4	< 0.001
注: IPW, 逆概率加权法；OW, 重叠权重法；oCBPS, 最优协变量均衡法；EB, 熵均衡法；SBW, 稳定权重值均衡法。 Note : IPW, inverse probability weight; OW, overlap weights; oCBPS, optimal covariate balancing; EB, entropy balancing; SBW, stable weights that balance covariates.

下载: 导出CSV

参考文献(21)

[1]	Rosenbaum PR. Observational studies (2nd ed.)[Z]. New York: Springer, 2002.
[2]	Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects[J]. Biometrika, 1983, 70(1): 41-55. DOI: 10.1093/biomet/70.1.41.
[3]	Robins JM, Rotnitzky A, Zhao LP. Estimation of regression coefficients when some regressors are not always observed[J]. J Am Stat Assoc, 1994, 89(427): 846-866. DOI: 10.1080/01621459.1994.10476818.
[4]	Hirano K, Imbens GW, Ridder G. Efficient estimation of average treatment effects using the estimated propensity score[J]. Econometrica, 2003, 71(4): 1161-1189. DOI: 10.1111/1468-0262.00442.
[5]	Horvitz DG, Thompson DJ. A generalization of sampling without replacement from a finite universe[J]. J AM Stat Assoc, 1952, 47(260): 663-685. DOI: 10.1080/01621459.1952.10483446.
[6]	Chesnaye NC, Stel VS, Tripepi G, et al. An introduction to inverse probability of treatment weighting in observational research[J]. Clin Kidney J, 2022, 15(1): 14-20. DOI: 10.1093/ckj/sfab158.
[7]	Ju C, Schwab J, van der Laan MJ. On adaptive propensity score truncation in causal inference[J]. Stat Methods Med Res, 2019, 28(6): 1741-1760. DOI: 10.1177/0962280218774817.
[8]	McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies[J]. Psychol Methods, 2004, 9(4): 403-425. DOI: 10.1037/1082-989X.9.4.403.
[9]	Hainmueller J. Entropy balancing for causal effects: A multivariate reweighting method to produce balanced samples in observational studies[J]. Political Analysis, 2011, 20(1): 25-46. DOI: 10.1093/pan/mpr025.
[10]	Zubizarreta JR. Stable weights that balance covariates for estimation with incomplete outcome data[J]. J Am Stat Assoc, 2015, 110(511): 910-922. DOI: 10.1080/01621459.2015.1023805.
[11]	Li F, Morgan KL, Zaslavsky AM. Balancing covariates via propensity score weighting[J]. J AM Stat Assoc, 2018, 113(521): 390-400. DOI: 10.1080/01621459.2016.1260466.
[12]	Fan JQ, Imai K, Lee I, et al. Optimal covariate balancing conditions in propensity score estimation[J]. J Bus Econ Stat, 2023, 41(1): 97-110. DOI: 10.1080/07350015.2021.2002159.
[13]	Crump RK, Hotz VJ, Imbens GW, et al. Dealing with limited overlap in estimation of average treatment effects[J]. Biometrika, 2009, 96(1): 187-199. DOI: 10.1093/biomet/asn055.
[14]	Li L, Greene T. A weighting analogue to pair matching in propensity score analysis[J]. Int J Biostat, 2013, 9(2): 215-234. DOI: 10.1515/ijb-2012-0030.
[15]	Bin YS, Marshall NS, Glozier N. Secular trends in adult sleep duration: a systematic review[J]. Sleep Med Rev, 2012, 16(3): 223-230. DOI: 10.1016/j.smrv.2011.07.003.
[16]	Piovezan RD, Hirotsu C, Feres MC, et al. Obstructive sleep apnea and objective short sleep duration are independently associated with the risk of serum vitamin D deficiency[J]. PLoS One, 2017, 12(7): e0180901. DOI: 10.1371/journal.pone.0180901.
[17]	Bertisch SM, Sillau S, De Boer IH, et al. 25-hydroxyvitamin D concentration and sleep duration and continuity: multi-ethnic study of atherosclerosis[J]. Sleep, 2015, 38(8): 1305-1311. DOI: 10.5665/sleep.4914.
[18]	Shiue I. Low vitamin D levels in adults with longer time to fall asleep: US NHANES, 2005-2006[J]. Int J Cardiol, 2013, 168(5): 5074-5075. DOI: 10.1016/j.ijcard.2013.07.195.
[19]	Thomas LE, Li F, Pencina MJ. Overlap weighting: a propensity score method that mimics attributes of a randomized clinical trial[J]. JAMA, 2020, 323(23): 2417-2418. DOI: 10.1001/jama.2020.7819.
[20]	Zhou YJ, Matsouaka RA, Thomas L. Propensity score weighting under limited overlap and model misspecification[J]. Stat Methods Med Res, 2020, 29(12): 3721-3756. DOI: 10.1177/0962280220940334.
[21]	Pereira-Santos M, Costa PR, Assis AM, et al. Obesity and vitamin D deficiency: a systematic review and meta-analysis[J]. Obes Rev, 2015, 16(4): 341-349. DOI: 10.1111/obr.12239.