老年人脉压变化与全因死亡关联的贝叶斯联合模型应用研究

谢纬华; 余小金; 戴品远; 孙金芳; 王莉娜; 覃玉; 武鸣; 赵健

doi:10.16462/j.cnki.zhjbkz.2021.01.014

老年人脉压变化与全因死亡关联的贝叶斯联合模型应用研究

doi: 10.16462/j.cnki.zhjbkz.2021.01.014

1.
210009 南京，东南大学公共卫生学院流行病与卫生统计学系
2.
210009 南京，江苏省疾病预防控制中心慢性非传染病防制所

基金项目:

国家自然科学基金 81673274

详细信息

通讯作者:
余小金，E-mail：xiaojinyu@seu.edu.cn

中图分类号: R181
计量
- 文章访问数: 653
- HTML全文浏览量: 324
- PDF下载量: 74
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-11
- 修回日期: 2020-11-10
- 刊出日期: 2021-01-10

Application of a bayesian joint model for the association of changes in pulse pressure and all-cause mortality in the elderly

1.
Department of Epidemiology and Health Statistics, School of Public Health, Southeast University, Nanjing 210009, China
2.
Department of Chronic Non-Communicable Disease Control and Prevention, Jiangsu Provincial Center for Disease Control and Prevention, Nanjing 210009, China

Funds:

National Natural Science Foundation of China 81673274

More Information

Corresponding author: YU Xiao-jin, E-mail: xiaojinyu@seu.edu.cn

摘要

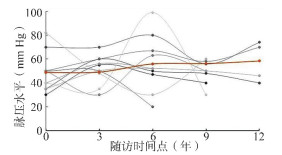
摘要: 目的以老年人脉压变化与全因死亡的关联研究为背景，探讨贝叶斯联合模型拟合相互关联的纵向结局与生存结局时的应用策略和统计性能，为类似特征资料的分析提供方法学指导。方法本研究以自然三次样条函数拟合纵向测量脉压的非线性混合效应模型，并采用B样条法构建全死因生存结局的基线风险函数，通过共享的随机效应关联两个过程建立贝叶斯联合模型，运用Gibbs抽样进行模型参数计算，并将贝叶斯联合模型结果与经典两步法联合模型进行比较。结果贝叶斯联合模型结果显示基线脉压越高(α₁=0.72, 95% CI: 0.43~1.13)，第0~3年、3~6年、6~9年脉压升高越快(α₂₁=0.34, 95% CI: 0.20~0.45); α₂₂=0.45, 95% CI: 0.10~0.75; α₂₃=0.42, 95% CI: 0.24~0.62)，老年人全因死亡风险越高。贝叶斯法和两步法联合模型在参数点估计方向上具有一致性，贝叶斯法的区间宽度大于两步法。结论当纵向与生存数据存在关联时，贝叶斯联合模型是对纵向与生存数据联合分析合理有效的统计方法。研究显示，老年人基线脉压过高和脉压升高过快均会造成更高的死亡风险。
- 纵向数据 /
- 生存数据 /
- 老年人脉压 /
- 全因死亡 /
- 贝叶斯联合模型 /
- 两步法联合模型
Abstract: Objective To explore application strategies and statistical performance when fitting Bayesian joint models to interrelate longitudinal and survival outcomes, and provide methodological guidance for the analysis of similar data. Methods A nonlinear mixed-effects model of longitudinally measured pulse pressure was fitted with a natural cubic spline function, and a B-spline method was used to construct the baseline hazard function for all-cause survival data. A Bayesian joint model was established by associating two processes through shared random effects and Gibbs sampling was used to calculate model parameters. The results of Bayesian joint model were compared with the classical two-stage joint model. Results The Bayesian joint model showed a higher baseline pulse pressure (α₁=0.72, 95% CI: 0.43-1.13) and faster rise in pulse pressure in years 0 to 3, 3 to 6, and 6 to 9 (α₂₁=0.34, 95% CI: 0.20-0.45; α₂₂= 0.45, 95% CI: 0.10-0.75; α₂₃=0.42, 95% CI: 0.24-0.62), which may contribute to a higher risk of all-cause death in the elderly. Bayesian and two-stage joint models were consistent in the direction of parameter point estimates, with Bayesian interval widths greater than two-stage methods. Conclusions Bayesian joint model is a reasonably valid statistical method for joint analysis of longitudinal and survival data when there is an association between them. This study has shown that both high baseline pulse pressure and rapid increases in pulse pressure in older adults are associated with higher all-cause mortality.
- Longitudinal data /
- Survival data /
- Pulse pressure in the elderly /
- All-cause mortality /
- Bayesian joint model /
- Two-stage joint model

HTML全文

图 1 老年人脉压水平随时间变化的轨迹

注：灰色线代表 10位老年人的脉压，橙色线表示总体人群平均脉压。

Figure 1. The changing trajectories of pulse pressure in the elderly

下载: 全尺寸图片幻灯片

图 2 贝叶斯联合模型与两步法联合模型的协变量参数估计结果比较

Figure 2. Comparison of covariable parameter estimation results between Bayesian and two-stage joint model

下载: 全尺寸图片幻灯片

表 1 老年健康影响因素跟踪调查数据库研究人群基线情况描述

Table 1. Baseline descriptions of the study population in the CLHLS

预测变量	例数[n (%)]	预测变量	例数[n (%)]
性别		心脑血管疾病
男	6 355 (46.41)	是	1 476 (10.78)
女	7 337 (53.59)	否	12 216 (89.22)
民族		呼吸系统疾病
汉族	12 933 (94.48)	是	2 799 (20.44)
其他民族	759 (5.52)	否	10 893 (79.56)
年龄(岁)		心理健康水平
60~	4 880 (35.64)	较低	6 873 (52.79)
≥80	8 812 (64.36)	较高	6 146 (47.20)
是否受过教育		主食摄入量
是	5 689 (41.77)	较少	6 866 (50.15)
否	7 930 (58.22)	较多	6 826 (49.85)
60岁前职业		水果摄入频率
脑力劳动为主	1 313 (9.63)	较少	8 083 (59.04)
体力劳动为主	12 323 (90.37)	较多	5 608 (40.97)
居住地类型		蔬菜摄入频率
城镇	6 356 (46.42)	较少	6 689 (48.85)
乡村	7 336 (53.58)	较多	7 002 (51.14)
婚姻状态		肉类摄入频率
未婚、丧偶、分居	9 035 (65.99)	较少	6 954 (50.79)
已婚并与配偶同居	4 657 (34.01)	较多	6 737 (49.21)
结婚次数(次)		鱼类摄入频率
≤1	11 995 (89.11)	较少	9 051 (66.10)
≥2	1 466 (10.89)	较多	4 641 (33.90)
主要经济来源		鸡蛋摄入频率
自己	5 046 (36.85)	较少	7 460 (54.49)
他人	8 646 (63.15)	较多	6 232 (45.52)
自平经济水平		豆制品摄入频率
较差或一般	10 385 (76.02)	较少	6 915 (50.50)
较好	3 276 (23.98)	较多	6 777 (49.49)
主食类型		腌菜摄入频率
大米	8 988 (65.64)	较少	7 266 (53.07)
其他主食	4 704 (34.36)	较多	6 426 (46.94)
吸烟		白糖摄入频率
是	4 720 (35.40)	较少	9 089 (66.38)
否	8 613 (64.60)	较多	4 603 (33.62)
喝酒		饮茶频率
是	4 021 (31.24)	较少	6 878 (50.23)
否	8 850 (68.76)	较多	6 813 (49.77)
日常锻炼		大蒜摄入频率
是	4 882 (39.39)	较少	7 775 (56.78)
否	7 512 (60.61)	较多	5 917 (43.21)
高血压		日常休闲活动
是	3 786 (27.65)	较少	7 656 (55.92)
否	9 906 (72.35)	较多	6 036 (44.08)
糖尿病		认知功能评分
是	593 (4.33)	较低	6 539 (47.76)
否	13 102 (95.67)	较高	7 153 (52.24)

下载: 导出CSV

参考文献(21)

[1]	刘磊磊.不同血压指标与全因死亡关系的队列研究[D].郑州: 郑州大学, 2019. Liu LL. Cohort study on the relationship between different blood pressure indexes and all-cause death [D]. Zhengzhou: Zhengzhou University, 2019.
[2]	Lv YB, Gao X, Yin ZX, et al. Revisiting the association of blood pressure with mortality in oldest old people in China: community based, longitudinal prospective study [J]. BMJ, 2018, 361(1):k2158. DOI: 10.1136/bmj.k2158.
[3]	赛晓勇.西安地区军队离退休干部全死因与脑卒中相关因素的流行病学研究[D].西安: 第四军医大学, 2007. Sai XY. An epidemiological study on all causes of death and related factors of stroke among retired military cadres in Xi'an [D]. Xi'an: The Fourth Military Medical University, 2007.
[4]	Sardarinia M, Akbarpour S, Lotfaliany M, et al. Risk Factors for Incidence of Cardiovascular Diseases and All-Cause Mortality in a Middle Eastern Population over a Decade Follow-up: Tehran Lipid and Glucose Study [J]. PLoS One, 2016, 11(12):e0167623. DOI: 10.1371/journal.pone.0167623.
[5]	Wu L, Liu W, Yi G, et al. Analysis of Longitudinal and Survival Data: Joint Modeling, Inference Methods, and Issues [J]. Braz J Probab Stat, 2012, (1):1-17. DOI: 10.1155/2012/640153.
[6]	Qiu FY, Stein CM, Elston RC, et al. Joint modeling of longitudinal data and discrete-time survival outcome [J]. Stat Methods Med Res, 2016, 25(4):1512-1526. DOI: 10.1177/0962280213490342.
[7]	Taylor JMG, Park Y, Ankerst DP, et al. Real-Time Individual Predictions of Prostate Cancer Recurrence Using Joint Models [J]. Biometrics, 2013, 69(1):206-213. DOI: 10.1111/j.1541-0420.2012.01823.x.
[8]	Tang AM, Zhao XQ, Tang NS. Bayesian variable selection and estimation in semiparametric joint models of multivariate longitudinal and survival data [J]. Biom J, 2017, 59(1): 57-78. DOI: 10.1002/bimj.201500070.
[9]	Kohler M, Umlauf N, Beyerlein A., et al. Flexible Bayesian additive joint models with an application to type 1 diabetes research [J]. Biom J, 2017, 59(6):1144-1165. DOI: 10.1002/bimj.201600224.
[10]	Lawrence GA, Boye ME, Crowther MJ, et al. Joint modeling of survival and longitudinal non-survival data: current methods and issues. Report of the DIA Bayesian joint modeling working group [J]. Stat Med, 2015, 34(14):2181-2195. DOI: 10.1002/sim.6141.
[11]	曾毅.中国老年健康影响因素跟踪调查(1998-2012)及相关政策研究综述(上) [J].老龄科学研究, 2013, 1(1):65-72. DOI: CNKI:SUN:LLKX.0.2013-01-009. Zeng Y. A follow-up survey of health factors of the elderly in China (1998-2012) and a summary of related polic research (part Ⅰ) [J]. Scientific Research on Aging, 2013, 1(1):65-72. DOI: CNKI:SUN:LLKX.0.2013-01-009.
[12]	曾毅.中国老年健康影响因素跟踪调查(1998-2012)及相关政策研究综述(下) [J].老龄科学研究, 2013, 1(2):63-71. DOI: 10.3969/j.issn.2095-5898.2013.02.008. Zeng Y. A follow-up survey of health factors of the elderly in China (1998-2012) and a summary of related polic research (part Ⅱ) [J]. Scientific Research on Aging, 2013, 1(2):63-71. DOI: 10.3969/j.issn.2095-5898.2013.02.008.
[13]	Zeng Y, Feng QS, Hesketh T, et al. Survival, disabilities in activities of daily living, and physical and cognitive functioning among the oldest-old in China: a cohort study [J]. Lancet, 2017, 389(10079):1619-1629. DOI: 10.1016/S0140-6736(17)30548-2.
[14]	Rizopoulos D. The R Package JMbayes for Fitting Joint Models for Longitudinal and Time-to-Event Data Using MCMC [J]. J Stat Softw, 2016, 72(7):1-46. DOI: 10.18637/jss.v072.i07.
[15]	Zhao L, Song Y, Dong P, et al. Brachial pulse pressure and cardiovascular or all-cause mortality in the general population: a meta-analysis of prospective observational studies [J]. J Clin Hypertens, 2014, 16(9):678-685. DOI: 10.1111/jch.12375.
[16]	Rizopoulos D. JM: An R Package for the Joint Modelling of Longitudinal and Time-to-Event Data [J]. J Stat Softw, 2010, 35(9):1-33. DOI: 10.18637/jss.v035.i09
[17]	Rizopoulos D, Ghosh P. A Bayesian semiparametric multivariate joint model for multiple longitudinal outcomes and a time-to-event [J]. Stat Med, 2011, 30(12):1366-1380. DOI: 10.1002/sim.4205.
[18]	Albert PS, Shih JH. An approach for jointly modeling multivariate longitudinal measurements and discrete time-to-event data [J]. Ann Appl Stat, 2010, 4(3):1517-1532. DOI: 10.1214/10-aoas339.
[19]	Lin H, Mcculloch CE, Mayne ST. Maximum likelihood estimation in the joint analysis of time-to-event and multiple longitudinal variables [J]. Stat Med, 2002, 21(16):2369-2382. DOI: 10.1002/sim.1179.
[20]	Proust-Lima C, Joly P, Dartigues JF, et al. Joint modelling of multivariate longitudinal outcomes and a time-to-event: a nonlinear latent class approach [J]. Comput Stat Data An, 2009, 53(4):1142-1154. DOI: 10.1016/j.csda.2008.10.017.
[21]	Hickey GL, Philipson P, Jorgensen A, et al. Joint modelling of time-to-event and multivariate longitudinal outcomes: recent developments and issues [J]. BMC Med Res Methodol. 2016, 16(1):117. DOI: 10.1186/s12874-016-0212-5.